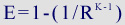The Otto Cycle
Increased compression, by a change in displacement, chamber volume, or both, increases torque throughout the RPM range, and is especially helpful at part-throttle. However, the increase is most effective in cases where the original compression ratio is relatively low. Adding 1 point of compression; e.g., 5.00-1 raised to 6.00-1, a change of +20% in ratio, increases efficiency by 9.0%, is more effective than the same percentage increase beginning with a higher ratio: 6.75-1 raised to 8.00-1 (19%) only increases efficiency by 6.8%.
A comparison based on a specific compression ratio increment (rather than a proportion) is even more revealing. Adding 1 point to a 5.50-1 engine adds 7.7%, but adding 1 point to a 7.00-1 engine only adds 5.2%.
“Efficiency” refers to the relative use made of the energy contained in the fuel, not the amount or percentage of fuel or air consumed. The efficiency assumes that no other changes are made when the compression ratio is altered, such as quench, valve shrouding, piston dome masking, etc. and that fuel of sufficient octane is used to permit the best ignition setting for maximum efficiency.
In practical terms, increasing the compression ratio sometimes alters other factors: breathing, quench, swirl, flame travel, &c. so the direct numerical comparison is not entirely accurate - higher ratios will generally show smaller improvements than indicated, but I have no method of including these factors in the calculations.
“Ideal” Otto-cycle model calculations use the traditional “adiabatic ratio of variable heats” for air and similar gasses (1.4) as the exponent (power). The error here is that there is always heat loss into the cylinder itself on compression, therefore a lower polytropic value should be substituted for 1.4. The exponent used for calculations here is 1.25, which is more realistic for normally aspirated 4-stroke internal combustion engines.
To use Table 1: locate the compression ratio in the top row. The cell directly below will show the efficiency calculated from the formula below, where E = efficiency, R = static (nominal) compression ratio, and K = 1.25.
To compare different compression ratios for efficiency, divide the Efficiency value of the new ratio by the Efficiency value of the original (already completed in Table 2, below. |